您可以创建自己的ScaleBase类来完成此操作。为了您的目的，我修改了here的示例（它生成了一个平方标度，而不是平方根标度）。另请参阅文档here。
请注意，要正确地执行此操作，您可能还应该创建自己的自定义滴答定位器;但我在这里没有这样做;我只是使用ax.set_yticks()手动设置主刻度和次刻度。

import matplotlib.scale as mscale
import matplotlib.pyplot as plt
import matplotlib.transforms as mtransforms
import matplotlib.ticker as ticker
import numpy as np

class SquareRootScale(mscale.ScaleBase):
    """
    ScaleBase class for generating square root scale.
    """
 
    name = 'squareroot'
 
    def __init__(self, axis, **kwargs):
        # note in older versions of matplotlib (<3.1), this worked fine.
        # mscale.ScaleBase.__init__(self)

        # In newer versions (>=3.1), you also need to pass in `axis` as an arg
        mscale.ScaleBase.__init__(self, axis)
 
    def set_default_locators_and_formatters(self, axis):
        axis.set_major_locator(ticker.AutoLocator())
        axis.set_major_formatter(ticker.ScalarFormatter())
        axis.set_minor_locator(ticker.NullLocator())
        axis.set_minor_formatter(ticker.NullFormatter())
 
    def limit_range_for_scale(self, vmin, vmax, minpos):
        return  max(0., vmin), vmax
 
    class SquareRootTransform(mtransforms.Transform):
        input_dims = 1
        output_dims = 1
        is_separable = True
 
        def transform_non_affine(self, a): 
            return np.array(a)**0.5
 
        def inverted(self):
            return SquareRootScale.InvertedSquareRootTransform()
 
    class InvertedSquareRootTransform(mtransforms.Transform):
        input_dims = 1
        output_dims = 1
        is_separable = True
 
        def transform(self, a):
            return np.array(a)**2
 
        def inverted(self):
            return SquareRootScale.SquareRootTransform()
 
    def get_transform(self):
        return self.SquareRootTransform()
 
mscale.register_scale(SquareRootScale)

fig, ax = plt.subplots(1)

ax.plot(np.arange(0, 9)**2, label='$y=x^2$')
ax.legend()

ax.set_yscale('squareroot')
ax.set_yticks(np.arange(0,9,2)**2)
ax.set_yticks(np.arange(0,8.5,0.5)**2, minor=True)

plt.show()

这是旧的，但我做了一个快速修复，因为我不想创建一个自定义的滴答定位器。如果你正在制作很多带有自定义比例的图，这可能是要走的路。如果您只需要一两个图，只需使用所需的比例绘制函数，然后设置刻度并更改标签会更快。

Nx = 100
x = np.linspace(0,50,Nx)
y = np.sqrt(x)

fig, ax = plt.subplots(1, 1)

plt.plot(np.sqrt(x), y)
ax.set_xticks([np.sqrt(x[i]) for i in range(0, Nx, Nx // 10)])
ax.set_xticklabels([str(round(x[i],0))[:-2] for i in range(0, Nx, Nx // 10)])
plt.xlabel('x')
plt.ylabel(r'y = $\sqrt{x}$')
plt.grid()
plt.show()

产生了情节

我喜欢lolopop的评论和tom的回答，一个更快更脏的解决方案是使用set_yticks和set_yticklabels，如下所示：

x = np.arange(2, 15, 2)
y = x * x

fig = plt.figure()
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)

ax1.plot(x,y)

ax2.plot(x, np.sqrt(y))
ax2.set_yticks([2,4,6,8,10,12,14])
ax2.set_yticklabels(['4','16','36','64','100','144','196'])

使用matplotlib.scale.FuncScale。它本质上是一个一行程序，取尺度函数和它的逆。如果你想让它看起来好看，你可以添加自定义刻度等等：

import matplotlib
import matplotlib.pyplot as plt

# Start a figure.
ax: plt.Axes
fig: plt.Figure
fig, ax = plt.subplots(1, 1)

# Set the y axis scale of the figure to a sqrt scale.
func = lambda e: e**0.5
inv_func = lambda e: e**2
ax.set_yscale(matplotlib.scale.FuncScale(ax, (func, inv_func)))

# Demonstrate.
xs = [1, 2, 3, 4, 5]
ys = [1, 4, 64, 16, 25]
ax.plot(xs, ys)
plt.show()

Matplotlib现在提供了一个powlaw规范。因此，将功率设置为0.5应该就可以了！
C.f. Matplotlib Powerlaw norm
他们的例子：

"""
Demonstration of using norm to map colormaps onto data in non-linear ways.
"""

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as colors
from matplotlib.mlab import bivariate_normal

N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]

'''
PowerNorm: Here a power-law trend in X partially obscures a rectified
sine wave in Y. We can remove gamma to 0.5 should do the trick using  PowerNorm.
'''
X, Y = np.mgrid[0:3:complex(0, N), 0:2:complex(0, N)]
Z1 = (1 + np.sin(Y * 10.)) * X**(2.)

fig, ax = plt.subplots(2, 1)

pcm = ax[0].pcolormesh(X, Y, Z1, norm=colors.PowerNorm(gamma=1./2.),
                       cmap='PuBu_r')
fig.colorbar(pcm, ax=ax[0], extend='max')

pcm = ax[1].pcolormesh(X, Y, Z1, cmap='PuBu_r')
fig.colorbar(pcm, ax=ax[1], extend='max')
fig.show()

这是绘制

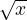
的简单方法

import numpy as np
from matplotlib import pyplot as plt

plt.rcParams["figure.dpi"] = 140

fig, ax = plt.subplots()
ax.spines["left"].set_position("zero")
ax.spines["bottom"].set_position("zero")
ax.spines["right"].set_color("none")
ax.spines["top"].set_color("none")
ax.xaxis.set_ticks_position("bottom")
ax.yaxis.set_ticks_position("left")

origin = [0, 0]

# 45
plt.plot(
    np.linspace(0, 1, 1000),
    np.sqrt(np.linspace(0, 1, 1000)),
    color="k",
)

ax.set_aspect("equal")
plt.xlim(-0.25, 1)
plt.ylim(0, 1)
plt.yticks(ticks=np.linspace(0, 1, 6))
plt.show()